رگرسیون خطی چیست؟
رگرسیون خطی یک روش تحلیل داده است که با استفاده از یک دادهٔ شناخته‌شده و مرتبط، مقدار یک دادهٔ ناشناخته را پیش‌بینی می‌کند. این روش متغیر وابسته (ناشناخته) و متغیر مستقل (شناخته‌شده) را به‌صورت یک معادلهٔ خطی مدل‌سازی می‌کند. برای مثال، اگر داده‌هایی از درآمد و هزینه‌های سال گذشته داشته باشید، رگرسیون خطی این رابطه را تحلیل کرده و مثلاً نتیجه می‌گیرد که هزینه‌ها نصف درآمد هستند. سپس می‌تواند هزینهٔ آینده را با نصف‌کردن درآمد آینده پیش‌بینی کند.
رگرسیون خطی چه اهمیتی دارد؟
مدل‌های رگرسیون خطی ساده هستند و فرمول‌های ریاضی قابل‌فهمی برای پیش‌بینی ارائه می‌دهند. این روش یک تکنیک آماری تثبیت‌شده است و به‌راحتی در نرم‌افزارها پیاده‌سازی می‌شود. کسب‌وکارها از آن برای تبدیل داده‌های خام به اطلاعات کاربردی استفاده می‌کنند. دانشمندان در حوزه‌هایی مثل زیست‌شناسی، علوم رفتاری، محیط‌زیست و علوم اجتماعی از رگرسیون خطی برای تحلیل مقدماتی داده‌ها و پیش‌بینی روندهای آینده بهره می‌برند. بسیاری از روش‌های علم داده، از جمله یادگیری ماشین و هوش مصنوعی، از این تکنیک برای حل مسائل پیچیده استفاده می‌کنند.
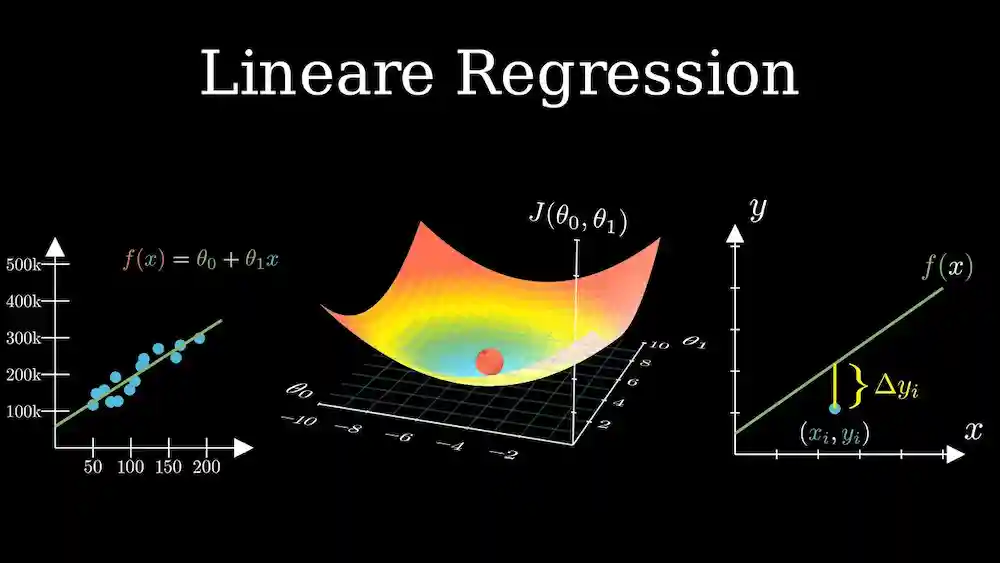
رگرسیون خطی چگونه کار می‌کند؟
در ساده‌ترین حالت، رگرسیون خطی تلاش می‌کند یک خط بین دو متغیر x و y رسم کند. متغیر مستقل x روی محور افقی قرار می‌گیرد و به آن متغیر توضیحی یا پیش‌بینی‌کننده نیز گفته می‌شود. متغیر وابسته y روی محور عمودی رسم می‌شود و می‌توان آن را متغیر پاسخ یا پیش‌بینی‌شده هم نامید.
مراحل انجام رگرسیون خطی
در ساده‌ترین حالت، معادلهٔ خط بین y و x به‌شکل y = c*x + m است؛ که در آن c و m برای همهٔ مقادیر ممکن x و y ثابت هستند. فرض کنید داده‌های ورودی (x, y) شامل (۱،۵)، (۲،۸) و (۳،۱۱) باشند. برای شناسایی مدل رگرسیون خطی، مراحل زیر انجام می‌شوند:
- یک خط مستقیم رسم می‌شود و رابطه بین ۱ و ۵ بررسی می‌شود.
- جهت خط به‌گونه‌ای تنظیم می‌شود که سایر نقاط مانند (۲،۸) و (۳،۱۱) نیز روی آن قرار گیرند.
- معادلهٔ خط به‌صورت y = 3*x + 2 شناسایی می‌شود.
- سپس می‌توان پیش‌بینی کرد که وقتی x برابر ۴ باشد، y برابر ۱۴ خواهد بود.
رگرسیون خطی در یادگیری ماشین چیست؟
در یادگیری ماشین، الگوریتم‌ها داده‌های بزرگ را تحلیل کرده و به‌صورت معکوس از داده‌ها برای محاسبهٔ معادلهٔ رگرسیون خطی استفاده می‌کنند. دانشمندان داده ابتدا الگوریتم را با داده‌های برچسب‌خورده آموزش می‌دهند و سپس از آن برای پیش‌بینی مقادیر ناشناخته بهره می‌برند. داده‌های واقعی بسیار پیچیده‌تر از مثال‌های ساده هستند. به همین دلیل، تحلیل رگرسیون خطی باید داده‌ها را به‌گونه‌ای تغییر دهد که چهار فرض زیر برقرار باشند:
۱. رابطهٔ خطی
بین متغیر مستقل و وابسته باید رابطه‌ای خطی وجود داشته باشد. برای بررسی این رابطه، دانشمندان داده از نمودار پراکندگی استفاده می‌کنند تا ببینند نقاط x و y روی یک خط قرار دارند یا نه. اگر چنین نبود، می‌توان از توابع غیرخطی مانند ریشه‌ٔ دوم یا لگاریتم برای تبدیل رابطه به شکل خطی استفاده کرد.
۲. استقلال باقی‌مانده‌ها
باقی‌مانده‌ها برای بررسی دقت پیش‌بینی به کار می‌روند. باقی‌مانده تفاوت بین مقدار واقعی و مقدار پیش‌بینی‌شده است. این باقی‌مانده‌ها نباید الگوی مشخصی داشته باشند؛ مثلاً نباید با گذر زمان بزرگ‌تر شوند. برای بررسی استقلال باقی‌مانده‌ها می‌توان از آزمون‌هایی مثل آزمون دوربین-واتسون (Durbin-Watson) استفاده کرد. همچنین می‌توان از داده‌های ساختگی برای جایگزینی نوسانات خاص، مثل داده‌های فصلی، بهره گرفت.
نرمال بودن
تکنیک‌های گرافیکی مانند نمودارهای Q-Q برای بررسی اینکه آیا باقی‌مانده‌ها به‌طور نرمال توزیع شده‌اند یا نه، استفاده می‌شوند. باقی‌مانده‌ها باید در امتداد یک خط قطری در مرکز نمودار قرار گیرند. اگر باقی‌مانده‌ها نرمال نباشند، می‌توان داده‌ها را برای شناسایی داده‌های پرت یا مقادیری که غیرمعمول هستند آزمایش کرد. حذف این داده‌های پرت یا اعمال تغییرات غیرخطی می‌تواند مشکل را حل کند.
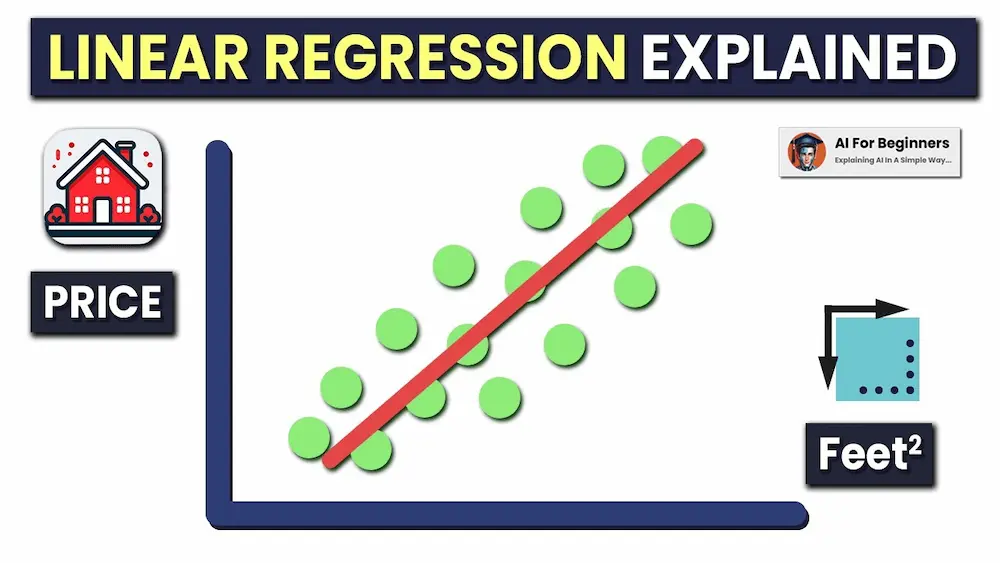
هم‌واریانسی (Homoscedasticity)
هم‌واریانسی فرض می‌کند که باقی‌مانده‌ها برای هر مقدار از x، واریانس یا انحراف معیار ثابتی از میانگین دارند. در غیر این صورت، نتایج تحلیل ممکن است دقیق نباشند. اگر این فرض برقرار نباشد، ممکن است لازم باشد متغیر وابسته تغییر یابد. از آنجا که واریانس به‌طور طبیعی در داده‌های بزرگ رخ می‌دهد، منطقی است که مقیاس متغیر وابسته تغییر کند. برای مثال، به‌جای استفاده از اندازه جمعیت برای پیش‌بینی تعداد ایستگاه‌های آتش‌نشانی در یک شهر، ممکن است از اندازه جمعیت برای پیش‌بینی تعداد ایستگاه‌های آتش‌نشانی به ازای هر نفر استفاده شود.
انواع رگرسیون خطی
برخی از انواع تحلیل رگرسیون برای پردازش داده‌های پیچیده مناسب‌تر از سایرین هستند. در اینجا چند مثال آورده شده است:
رگرسیون خطی ساده
رگرسیون خطی ساده با تابع خطی زیر تعریف می‌شود:
Y = β۰*X + β۱ + ε
که در آن β۰ و β۱ دو ثابت ناشناخته هستند که شیب رگرسیون را نشان می‌دهند و ε (اپسیلون) عبارت خطا است.
می‌توانید از رگرسیون خطی ساده برای مدل‌سازی رابطه بین دو متغیر استفاده کنید، مانند این موارد:
- بارش باران و بازده محصول
- سن و قد در کودکان
- دما و انبساط جیوه در دماسنج
رگرسیون خطی چندگانه
در تحلیل رگرسیون خطی چندگانه، مجموعه داده‌ها شامل یک متغیر وابسته و چندین متغیر مستقل است. معادله خط رگرسیون به‌گونه‌ای تغییر می‌کند که عوامل بیشتری را در بر می‌گیرد:
Y = β۰*X0 + β1X1 + β2X2 + …… + βnXn + ε
با افزایش تعداد متغیرهای پیش‌بینی‌کننده، ثابت‌های β نیز به‌طور متناسب افزایش می‌یابند.
رگرسیون خطی چندگانه روابط بین چندین متغیر و تأثیر آن‌ها بر یک نتیجه را مدل‌سازی می‌کند:
- بارش باران، دما و استفاده از کود بر بازده محصول
- رژیم غذایی و ورزش بر بیماری‌های قلبی
- رشد دستمزد و تورم بر نرخ وام مسکن
رگرسیون لجستیک
دانشمندان داده از رگرسیون لجستیک برای اندازه‌گیری احتمال وقوع یک رویداد استفاده می‌کنند. پیش‌بینی یک مقدار بین ۰ و ۱ است، که ۰ نشان‌دهنده احتمال کم وقوع رویداد و ۱ نشان‌دهنده احتمال زیاد وقوع آن است. معادلات لجستیک از توابع لگاریتمی برای محاسبه خط رگرسیون استفاده می‌کنند.
چند مثال از کاربرد رگرسیون لجستیک:
- احتمال پیروزی یا باخت در یک مسابقه ورزشی
- احتمال قبولی یا مردودی در یک آزمون
- احتمال اینکه یک تصویر میوه یا حیوان باشد
